注意力机制
什么是注意力机制
注意力机制就是对输入权重分配的关注,最开始使用到注意力机制是在编码器-解码器(encoder-decoder)中, 注意力机制通过对编码器所有时间步的隐藏状态做加权平均来得到下一层的输入变量:
注意力机制的通用表达式可以写为:
$$\boldsymbol{O} = \text{softmax}(\boldsymbol{Q}\boldsymbol{K}^\top)\boldsymbol{V}$$
注意力机制广义上可以理解成一个由查询项矩阵 $\boldsymbol{Q}$ 和所对应的键项 $\boldsymbol{K}$ 和 需加权平均的值项 $\boldsymbol{V}$ 所构成的一层感知机(softmax求和)。
这里我们可以从两个视角来看:
- 从工程学上理解
从工程学上简单理解,我们可以把注意力机制理解成从数据库(内存槽)Q中通过键K和值V得到输出O,由于V是输入,所以可以理解注意力机制的核心就是如何构建数据库Q和键值K的方法。
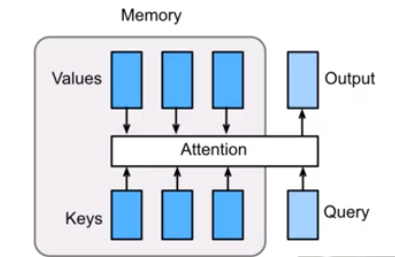
- 从算法上理解
从算法上来理解,我们可以把注意力机制和池化做类比,即将卷积神经网络中的池化看成一种特殊的平均加权的注意力机制,或者说注意力机制是一种具有对输入分配偏好的通用池化方法(含参数的池化方法)。
从构建查询项看注意力机制
最早的Attention的提出
在最早提出注意力机制的论文《Neural Machine Translation by Jointly Learning to Align and Translate》中,其主要是用来作翻译模型,解决翻译核对齐问题(论文采用了seq2seq+attention)。文中QK的计算表示:
$\boldsymbol{c}_{t’}$表示输出变量,$\boldsymbol{h}_t$为隐藏层,$\alpha_{t' t}$表示一个权重的概率分布,即QK得softmax值,这里得查询项矩阵Q采用了一个$\tanh(\boldsymbol{W}_s \boldsymbol{s} + \boldsymbol{W}_h \boldsymbol{h})$,所以$\sigma$其本质在是一个单层的感知机。由于这种注意力机制由Bahdanau在seq2seq中正式提出,也叫循环注意力机制,更加$\sigma$函数即其参数不同我们可以把注意力机制分成多种形式。
最基础形态的注意力机制
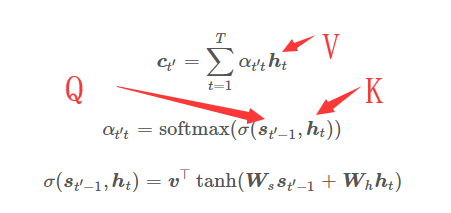
从上面我们将注意力机制抽象出来即:
$$\boldsymbol{c}_{t} = \sum_{t=1}^T\sigma(\boldsymbol{q},\boldsymbol{k}_t)\boldsymbol{h}_t$$q 为查询项, k 为键值项, h为隐含层输入变量,$\sigma$ 为变换函数,c表示模型输出的context vetor。
呃,趣味点的话也可以理解,输入的h,通过其对应键值k查询q,通过$\sigma$输出c
层次注意力(Hierarchical Attention Networks)
层次注意力由 Zichao Yang 提出,主要用于解决多层次问题,比如在文本分类中,我们可以把词作为一层,把段落作为一层,这样就有了多层,而且下面一层会对上一层有影响,因此建立了一种堆叠的层次注意力模型:
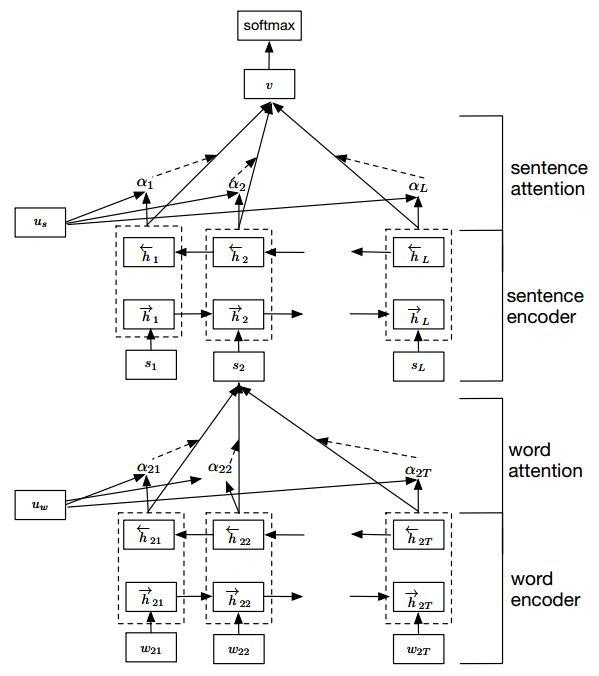
层次注意力机制就是堆叠了多个注意力模型,形成多层次注意力,其公式表达可以写成:
$$ \boldsymbol{c}_{t}^{(\boldsymbol{i+1})} = \sum_{t=1}^T\sigma^{(\boldsymbol{i})}(\boldsymbol{q}^{(\boldsymbol{i})},\boldsymbol{k}_t^{(\boldsymbol{i})})\boldsymbol{h}_t^{(\boldsymbol{i})},\\ \boldsymbol{h}_{t}^{(\boldsymbol{i})} = \boldsymbol{v}_{t}^{(\boldsymbol{i+1})}\boldsymbol{c}_{i}^{(\boldsymbol{t})}$$ $$\boldsymbol{h}_{0} = \boldsymbol{W}_{t}^{(0)}\boldsymbol{X}$$q 为查询项, k 为键值项, h为隐含层输入变量,$\sigma$ 为变换函数,c表示模型输出的context vetor,i表示层级。
什么意思呢?
首先,可以看到上层的注意力是以下层的输出作为输入,一层一层堆叠上去。
循环注意力
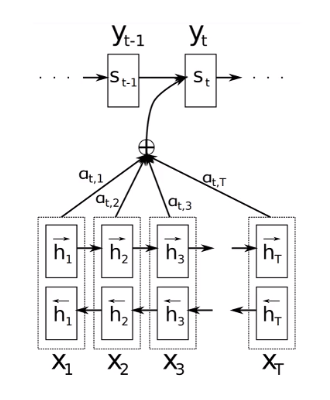
前面讲到,其实所谓的循环注意力模型就是最早提出的seq2seq的翻译模型:
$$ \begin{align} \boldsymbol{o}_{i} &= f(\boldsymbol{s}_{i}) \\ \boldsymbol{s}_{i} &= a(\boldsymbol{s}_{i-1},\boldsymbol{o}_{i-1},\boldsymbol{s}_{i}) \\ \boldsymbol{c}_{t'} &= \sum_{t=1}^T\alpha_{t' t}\boldsymbol{h}_t \\ \alpha_{t' t} &= \frac{\exp(e_{t' t})}{ \sum_{k=1}^T \exp(e_{t' k}) },\quad t=1,\ldots,T \\ e_{t' t} &= \sigma(\boldsymbol{s}_{t' - 1}, \boldsymbol{h}_t) \\ \sigma(\boldsymbol{s}_{t' - 1}, \boldsymbol{h}_t) &= \boldsymbol{V}^\top \tanh(\boldsymbol{W}_s \boldsymbol{s}_{t' - 1} + \boldsymbol{W}_h \boldsymbol{h}_t) \\ \end{align} $$其中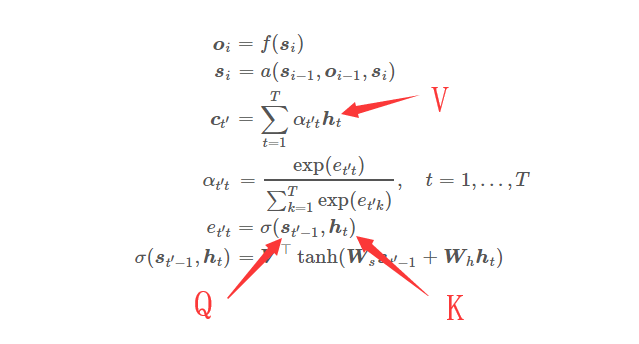
他的核心思想是将下一个输出的状态$\boldsymbol{s}_{t-1}$一起输入$\sigma$函数。
$\alpha_{t’ t}$就是注意力模型中的权重项,O表示输出,s表示解码器中的隐藏层变量,c表示context vetor, h表示编码器中的隐藏层变量。
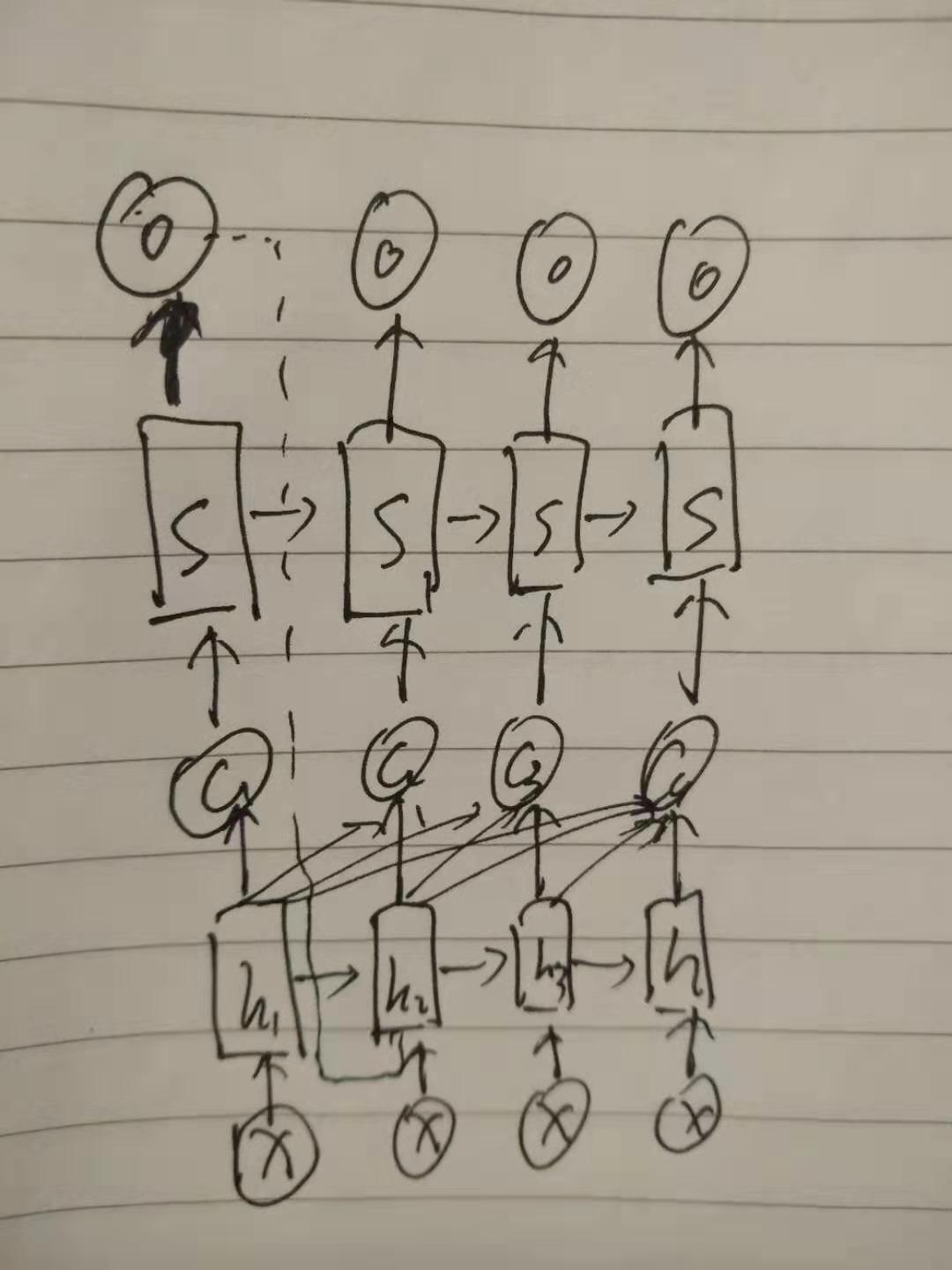
全局注意力模型(Gobal Attention)
全局注意力模型是由Minh-Thang Luong在2015年的《Effective Approaches to Attention-based Neural Machine Translation》中提出:
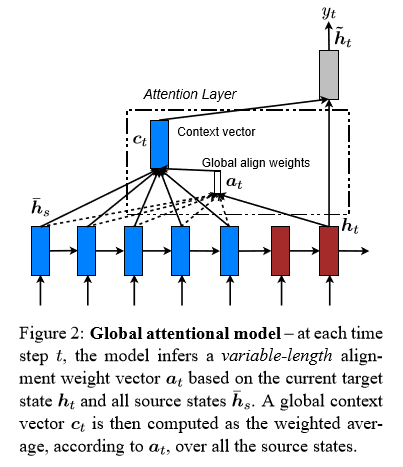
这个全局注意力模型是在循环注意力模型上左的改进,加个一层Global align weights(见上图),原循环注意力模型的键值项K是直接采用$\boldsymbol{h}_t$。其公式:
t 的编码器的隐藏变量,$\bar{\boldsymbol{h}_s}$表示所有的原时刻的编码器的隐藏变量score表示一种打分方式,其中论文中给出的是三种:$$ \text{score}(\boldsymbol{h}_t, \bar{\boldsymbol{h}_s)} = \begin{cases} \boldsymbol{h}_t^T \bar{\boldsymbol{h}_s}, &\text{dot}\\ \boldsymbol{h}_t^T \boldsymbol{W}_a \bar{\boldsymbol{h}_s}, &\text{general}\\ \boldsymbol{v}_a^T \text{tanh}(\boldsymbol{W}_a[\boldsymbol{h}_t;\bar{\boldsymbol{h}_s}]),&\text{concat} \end{cases} $$
dot表示点乘/点积,concat表示联接,即将两个变量连接起来,general是一般形式,中间加权重参数。
注: While our global attention approach is similar in spirit to the model proposed by Bahdanau et al. (2015), there are several key differences which reflect how we have both simplified and generalized from the original model.
局部注意力模型(Local Attention)
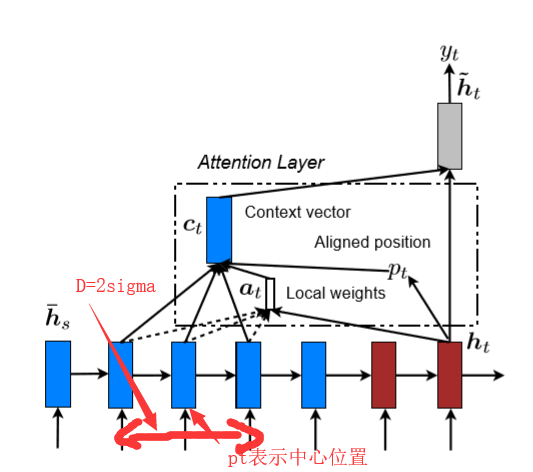
局部注意力模型其实是和全局注意力模型在同一篇论文提出的,局部注意力模型在全局注意力模型的基础上增加了aligned position帮助定位,使查询项Q和键值项K能专注部分信息:
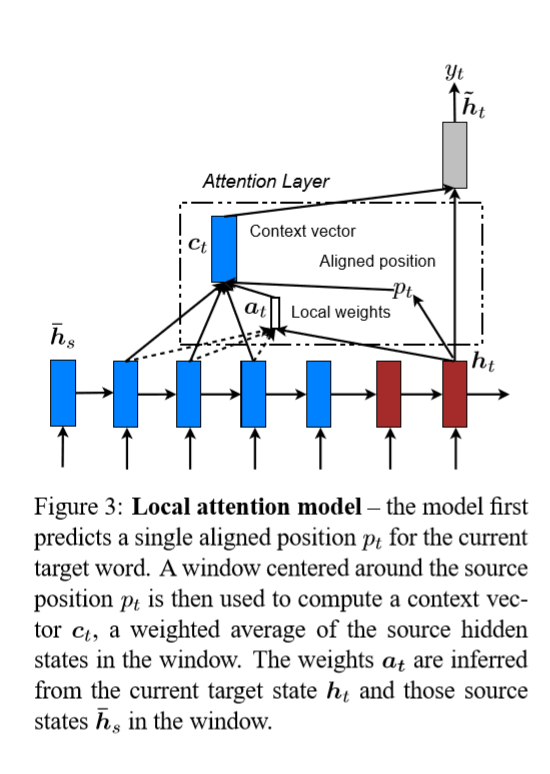
位置aligned position的公式:
S表示原句的长度,W和v为预测参数。
键值和查询项的权重:
$$\alpha_t(s) = \text{align}(\boldsymbol{h}_t, \bar{\boldsymbol{h}_s})\text{exp}(- \frac{(s-p_t)^2}{2\sigma^2})$$
$p_t$的范围是【0,S】,s为$p_t$窗体中间的正数,$\sigma=\frac{D}{2}$:
自注意力(Self Attention)
1、从n个输入直接输出n个输出,没有序列,每个输入对应着一个K,V,Q;
2、可以并行运算
多头注意力模型(Multi-Head Attention)
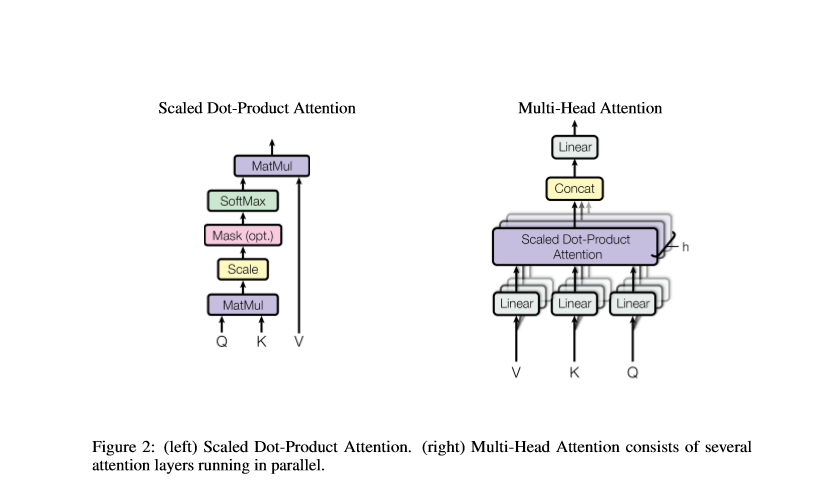
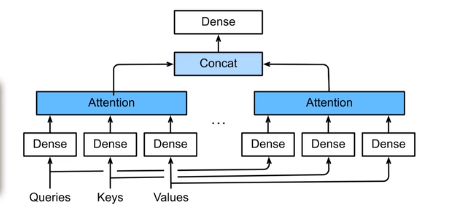
多头自注意力模型
其公式:
$$
\text{MultiHead}(Q,K,V) = \text{Concat}(\text{head1},...,\text{head}_h)\boldsymbol{W}^O
$$
$$
\text{head}_i = \text{Attention}(\boldsymbol{Q}\boldsymbol{W}_i^Q,\boldsymbol{K}\boldsymbol{W}_i^K,\boldsymbol{V}\boldsymbol{W}_i^V)
$$
$$
\text{Attention}(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}) = \text{softmax}(\frac{\boldsymbol{Q}\boldsymbol{K}^T}{\sqrt{d_k}})\boldsymbol{V}
$$
注意力模型的应用
Transformer
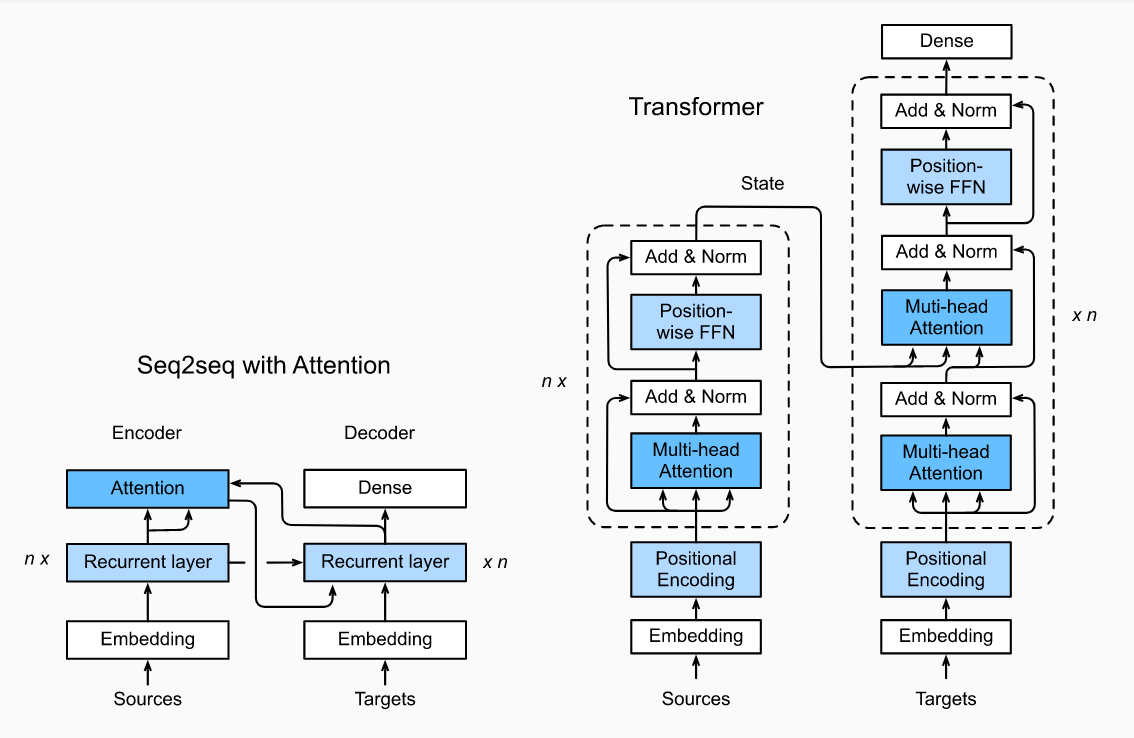
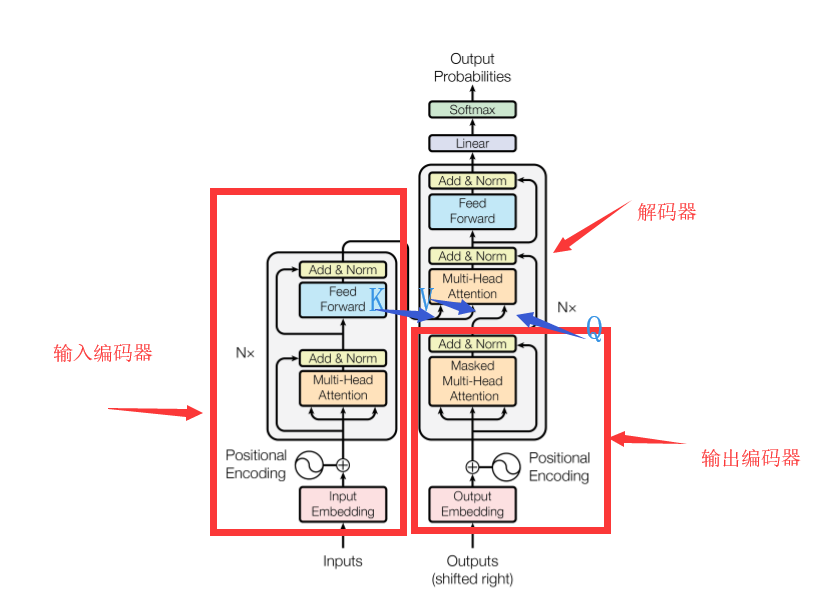
Transformer模型是 Google 团队在2017年《Attention is All You Need》中提出,Transformer模型在后面成为构成 BERT 的基石之一,那么我们来看看是怎么通过自注意力模型构建Transformer的: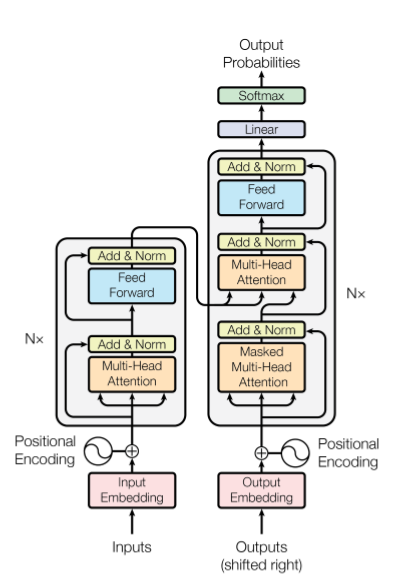
Transformer从结构上来说依然是个Encoder-Decoder模型,但是,它和传统的seq2seq主要有三点不同:
- 使用位置编码,也就是Positional Encoding代替序列信息。
- 使用Transformer Block来实现注意力机制
- 采用多头自注意力,可以并行运算
位置编码(Positional Encoding)
公式:
$$
\boldsymbol{P}_{i,2j} = \text{sin}(\frac{i}{10000^{2j/d}})
$$
$$
\boldsymbol{P}_{i,2j+1} = \text{sin}(\frac{i}{10000^{2j/d}})
$$
$$
\boldsymbol{H} = \boldsymbol{X} + \boldsymbol{P}, \\
\boldsymbol{X} \in \Bbb{R}, \boldsymbol{P} \in \Bbb{R}
$$
Position-wise FFN
- input(batch, seq len, fea size) 转换成 (batch*seq len, fea siz)
- 使用了两层MLP
- 最后的输出在转化为3-D
- 等于使用了一个$1\times1$的卷积层
- Layer Normalizaiton
Layer Normalization
Layer Normalization最早由 Jimmy Lei Ba 在2016年《Layer Normalization》一文中提出。
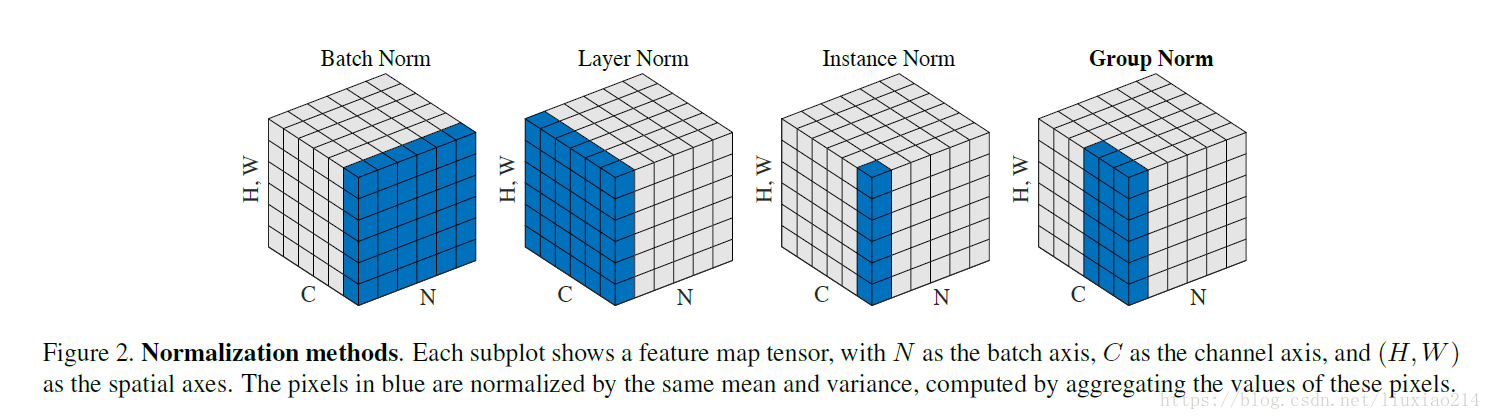
shape:[N, C, H, W]
N 代表batch长度,C代表通道数,H代表每层的隐藏单元数,W代表每层的权重;
- BatchNorm是在batch上,对NHW做归一化;
- LayerNorm在channel方向上,对CHW归一化;
- InstanceNorm在单个通道像素上,对HW做归一化;
- GroupNorm,有点类似LayerNorm,将channel分组,然后再做归一化;
BERT
BERT,全称 Bidirectional Encoder Representations from Transformers,是由
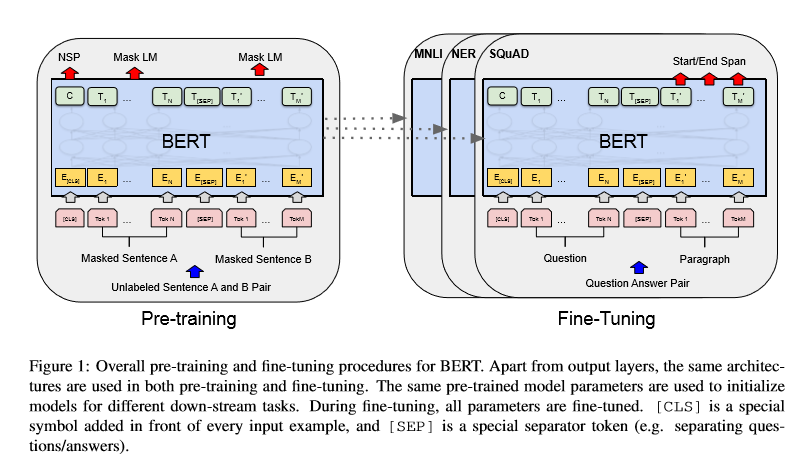
BERT特点:
- 使用
Transformer Block代替 RNN,通过堆叠Transformer Block将模型变深; - 使用随机 Mark 的方式训练;
- 使用双向编码的形式;
后面我们通过实现BERT来回归整个Attention系列:
BERT代码实现及解读
### 推荐系统中的注意力机制
Jun Xiao, et al. Attentional Factorization Machines: Learning the Weight of Feature Interactions via Attention Networks. 2017
参考文献
- https://github.com/d2l-ai/d2l-zh
- Neural Machine Translation by Jointly Learning to Align and Translate. Dzmitry Bahdanau, Kyunghyun Cho, and Yoshua Bengio. ICLR, 2015.
- Hierarchical attention networks for document classification. Zichao Yang et al. ACL, 2016.
- Effective approaches to attention-based neural machine translation. Minh-Thang Luong, Hieu Pham, and Christopher D Manning. EMNLP, 2015.
- Long Short-Term Memory-Networks for Machine Reading. Jianpeng Cheng, Li Dong and Mirella Lapata. EMNLP, 2016.
- Attention Is All You Need. Ashish Vaswani, et al. NIPS, 2017.


