每日一课 Kaggle 练习讲解
每周一道Kaggle题,学习机器学习!
今天给大家来讲讲《House Prices: Advanced Regression Techniques》(房价预测模型)的思路:
- (1) 数据可视化和数据分布变换
- (2) 缺省值处理
- (3) 数据特征变换
- (4) 数据建模及交叉检验
- (5) 模型组合
import numpy as np |
加载数据
去除ID
train_path = "http://kaggle.shikanon.com/house-prices-advanced-regression-techniques/train.csv" |
我们在分析之前要先了解个字段的意思:
train_df.columns |
Index(['Id', 'MSSubClass', 'MSZoning', 'LotFrontage', 'LotArea', 'Street',
'Alley', 'LotShape', 'LandContour', 'Utilities', 'LotConfig',
'LandSlope', 'Neighborhood', 'Condition1', 'Condition2', 'BldgType',
'HouseStyle', 'OverallQual', 'OverallCond', 'YearBuilt', 'YearRemodAdd',
'RoofStyle', 'RoofMatl', 'Exterior1st', 'Exterior2nd', 'MasVnrType',
'MasVnrArea', 'ExterQual', 'ExterCond', 'Foundation', 'BsmtQual',
'BsmtCond', 'BsmtExposure', 'BsmtFinType1', 'BsmtFinSF1',
'BsmtFinType2', 'BsmtFinSF2', 'BsmtUnfSF', 'TotalBsmtSF', 'Heating',
'HeatingQC', 'CentralAir', 'Electrical', '1stFlrSF', '2ndFlrSF',
'LowQualFinSF', 'GrLivArea', 'BsmtFullBath', 'BsmtHalfBath', 'FullBath',
'HalfBath', 'BedroomAbvGr', 'KitchenAbvGr', 'KitchenQual',
'TotRmsAbvGrd', 'Functional', 'Fireplaces', 'FireplaceQu', 'GarageType',
'GarageYrBlt', 'GarageFinish', 'GarageCars', 'GarageArea', 'GarageQual',
'GarageCond', 'PavedDrive', 'WoodDeckSF', 'OpenPorchSF',
'EnclosedPorch', '3SsnPorch', 'ScreenPorch', 'PoolArea', 'PoolQC',
'Fence', 'MiscFeature', 'MiscVal', 'MoSold', 'YrSold', 'SaleType',
'SaleCondition', 'SalePrice'],
dtype='object')
- MSSubClass: 建筑的等级,类型:类别型
- MSZoning: 区域分类,类型:类别型
- LotFrontage: 距离街道的直线距离,类型:数值型,单位:英尺
- LotArea: 地皮面积,类型:数值型,单位:平方英尺
- Street: 街道类型,类型:类别型
- Alley: 巷子类型,类型:类别型
- LotShape: 房子整体形状,类型:类别型
- LandContour: 平整度级别,类型:类别型
- Utilities: 公共设施类型,类型:类别型
- LotConfig: 房屋配置,类型:类别型
- LandSlope: 倾斜度,类型:类别型
- Neighborhood: 市区物理位置,类型:类别型
- Condition1: 主干道或者铁路便利程度,类型:类别型
- Condition2: 主干道或者铁路便利程度,类型:类别型
- BldgType: 住宅类型,类型:类别型
- HouseStyle: 住宅风格,类型:类别型
- OverallQual: 整体材料和饰面质量,类型:数值型
- OverallCond: 总体状况评价,类型:数值型
- YearBuilt: 建筑年份,类型:数值型
- YearRemodAdd: 改建年份,类型:数值型
- RoofStyle: 屋顶类型,类型:类别型
- RoofMatl: 屋顶材料,类型:类别型
- Exterior1st: 住宅外墙,类型:类别型
- Exterior2nd: 住宅外墙,类型:类别型
- MasVnrType: 砌体饰面类型,类型:类别型
- MasVnrArea: 砌体饰面面积,类型:数值型,单位:平方英尺
- ExterQual: 外部材料质量,类型:类别型
- ExterCond: 外部材料的现状,类型:类别型
- Foundation: 地基类型,类型:类别型
- BsmtQual: 地下室高度,类型:类别型
- BsmtCond: 地下室概况,类型:类别型
- BsmtExposure: 花园地下室墙,类型:类别型
- BsmtFinType1: 地下室装饰质量,类型:类别型
- BsmtFinSF1: 地下室装饰面积,类型:类别型
- BsmtFinType2: 地下室装饰质量,类型:类别型
- BsmtFinSF2: 地下室装饰面积,类型:类别型
- BsmtUnfSF: 未装饰的地下室面积,类型:数值型,单位:平方英尺
- TotalBsmtSF: 地下室总面积,类型:数值型,单位:平方英尺
- Heating: 供暖类型,类型:类别型
- HeatingQC: 供暖质量和条件,类型:类别型
- CentralAir: 中央空调状况,类型:类别型
- Electrical: 电力系统,类型:类别型
- 1stFlrSF: 首层面积,类型:数值型,单位:平方英尺
- 2ndFlrSF: 二层面积,类型:数值型,单位:平方英尺
- LowQualFinSF: 低质装饰面积,类型:数值型,单位:平方英尺
- GrLivArea: 地面以上居住面积,类型:数值型,单位:平方英尺
- BsmtFullBath: 地下室全浴室,类型:数值
- BsmtHalfBath: 地下室半浴室,类型:数值
- FullBath: 高档全浴室,类型:数值
- HalfBath: 高档半浴室,类型:数值
- BedroomAbvGr: 地下室以上的卧室数量,类型:数值
- KitchenAbvGr: 厨房数量,类型:数值
- KitchenQual: 厨房质量,类型:类别型
- TotRmsAbvGrd: 地上除卧室以外的房间数,类型:数值
- Functional: 房屋功用性评级,类型:类别型
- Fireplaces: 壁炉数量,类型:数值
- FireplaceQu: 壁炉质量,类型:类别型
- GarageType: 车库位置,类型:类别型
- GarageYrBlt: 车库建造年份,类别:数值型
- GarageFinish: 车库内饰,类型:类别型
- GarageCars: 车库车容量大小,类别:数值型
- GarageArea: 车库面积,类别:数值型,单位:平方英尺
- GarageQual: 车库质量,类型:类别型
- GarageCond: 车库条件,类型:类别型
- PavedDrive: 铺的车道情况,类型:类别型
- WoodDeckSF: 木地板面积,类型:数值型,单位:平方英尺
- OpenPorchSF: 开放式门廊区面积,类型:数值型,单位:平方英尺
- EnclosedPorch: 封闭式门廊区面积,类型:数值型,单位:平方英尺
- 3SsnPorch: 三个季节门廊面积,类型:数值型,单位:平方英尺
- ScreenPorch: 纱门门廊面积,类型:数值型,单位:平方英尺
- PoolArea: 泳池面积,类型:数值型,单位:平方英尺
- PoolQC:泳池质量,类型:类别型
- Fence: 围墙质量,类型:类别型
- MiscFeature: 其他特征,类型:类别型
- MiscVal: 其他杂项特征值,类型:类别型
- MoSold: 卖出月份,类别:数值型
- YrSold: 卖出年份,类别:数值型
- SaleType: 交易类型,类型:类别型
- SaleCondition: 交易条件,类型:类别型
数据处理和特征分析
#Saving Ids |
数据观察和可视化
更加常识,一般和房价最相关的是居住面积,也就是GrLivArea,我们查看下GrLivArea和SalePrice的关系
fig, ax = plt.subplots() |
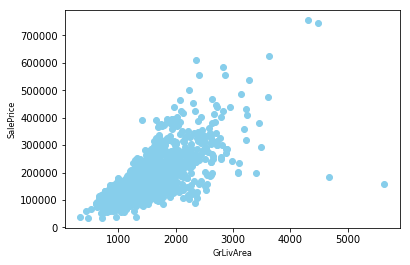
我们发现有个别值特别的偏离,GrLivArea有两个点在4000以上,但其价格不到200000,首先这种点特别少(不到总数的3%),我们把他作为异常值去掉(其实是否去掉我们可以多做几次实验来验证)
Kaggle的作者在这里有建议去掉:)
train_df.drop(train_df[(train_df['GrLivArea']>4000)&(train_df['GrLivArea']<30000)].index,inplace=True) |
fig, ax = plt.subplots() |
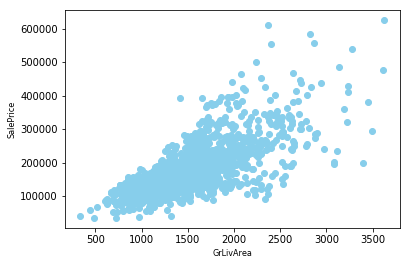
- 最后一行是
SalePrice, 我们可以看到她跟各变量的关系,还有各变量相互之间的关系观察数据分布
在机器学习中,对数据的认识是很重要的,他会影响我们的特征构建和建模,特别对于偏态分布,我们要做一些变换
# 统计表述 |
count 1456.000000
mean 180151.233516
std 76696.592530
min 34900.000000
25% 129900.000000
50% 163000.000000
75% 214000.000000
max 625000.000000
Name: SalePrice, dtype: float64
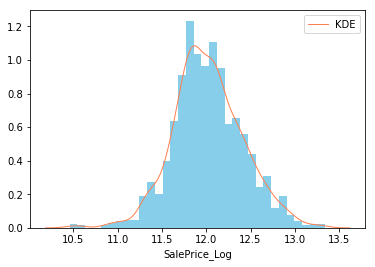
# 绘制分布图 |
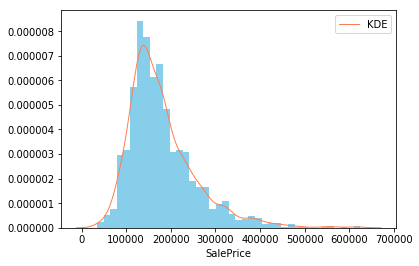
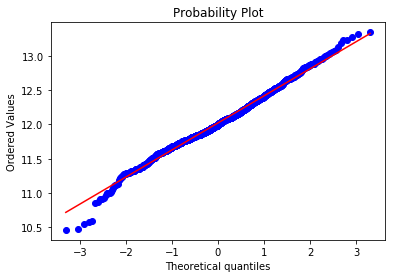
Q-Q图,全称 Quantile Quantile Plot,中文名叫分位数图,Q-Q图是一个概率图,用于比较观测与预测值之间的概率分布差异,这里的比较对象一般采用正态分布,Q-Q图可以用于检验数据分布的相似性,而P-P图是根据变量的累积概率对应于所指定的理论分布累积概率绘制的散点图,两者基本一样
# 绘制P-P图 |
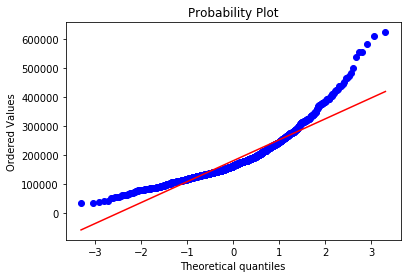
红色线是正态分布,蓝色线是我们的数据,可以看出,我们的数据头尾都严重偏离了正太分布,我们尝试对数据做变换,常用的变换有指数变换、对数变换、幂函数等。
# 对数变换 |
Skewness: 0.065449
Kurtosis: 0.666438
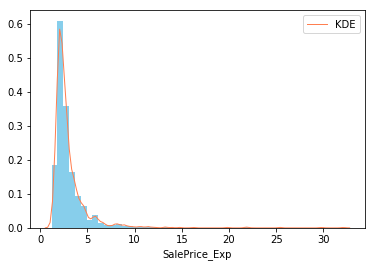
# 指数变换 |
Skewness: 6.060076
Kurtosis: 56.822460
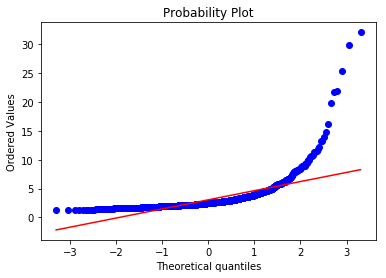
# 幂函数变换 |
Skewness: 0.810797
Kurtosis: 1.245798
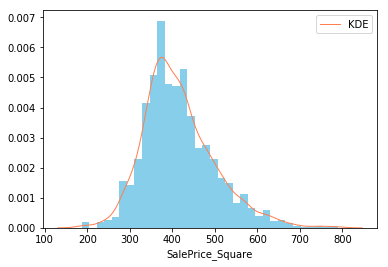
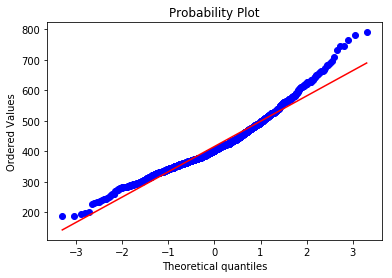
三个函数拟合对比,对数转换最吻合,但是我们知道对数意味着小于1的时候为负数,这明显和认知不符合,应该采用log(1+x),也就是log1p,保证了x数据的有效性,当x很小时,如: 10^{-16} ,由于太小超过数值有效性,用log(x+1)计算得到结果为0
# 对数变换 |
Skewness: 0.065460
Kurtosis: 0.666423
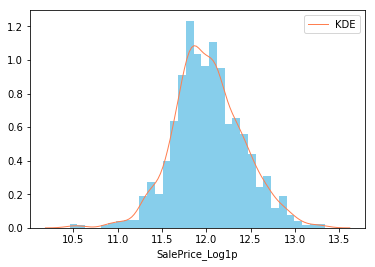
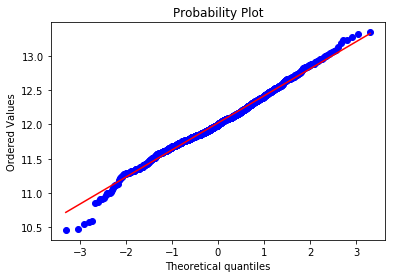
del train_df['SalePrice_Square'] |
del train_df["SalePrice"] |
将测试数据和训练数据联合一起进行特征分析
size_train_df = train_df.shape[0] |
缺失值处理
缺失值是实际数据分析很重要的一块,在实际生产中一直都会有大量的缺失值存在,如何处理好缺失值是很关键也很重要的一步。
常见的缺失值处理有:
- (1)把缺失值单独作为一类,比如对类别型用none。
- (2)采用平均数、中值、众数等特定统计值来填充缺失值。
- (3)采用函数预测等方法填充缺失值。
这里的各变量填充策略:
NA for ‘PoolQC’ means “No Pool”.
MiscFeature: NA means “None”
Alley: NA means “No alley access”
Fence: NA means “No fence”
FireplaceQu: NA means “No fireplace”
LotFrontage: fill missing values with median LotFrontage of neighborhood
GarageFinish: NA means “None”
GarageQual: NA means “None”
GarageCond: NA means “None”
GarageYrBlt: NA means 0
GarageType: NA means “None”
BsmtCond: NA means “None”
BsmtExposure: NA means “None”
BsmtQual: NA means “None”
BsmtFinType2: NA means “None”
BsmtFinType1: NA means “None”
MasVnrType: NA means “None”
MasVnrArea: NA means “0”
BsmtHalfBath: NA means “0”
BsmtFullBath: NA means “0”
BsmtFinSF1: NA means “0”
BsmtFinSF2: NA means “0”
BsmtUnfSF: NA means “0”
TotalBsmtSF: NA means “0”
GarageCars: NA means 0
GarageArea: NA means 0
data.count().sort_values().head(20) # 通过 count 可以找出有缺失值的数据 |
PoolQC 8
MiscFeature 105
Alley 198
Fence 570
FireplaceQu 1495
LotFrontage 2429
GarageCond 2756
GarageYrBlt 2756
GarageFinish 2756
GarageQual 2756
GarageType 2758
BsmtExposure 2833
BsmtCond 2833
BsmtQual 2834
BsmtFinType2 2835
BsmtFinType1 2836
MasVnrType 2891
MasVnrArea 2892
MSZoning 2911
BsmtFullBath 2913
dtype: int64
data_na = (data.isnull().sum() / len(data)) * 100 |
Text(0.5, 1.0, 'Percent missing data by feature')
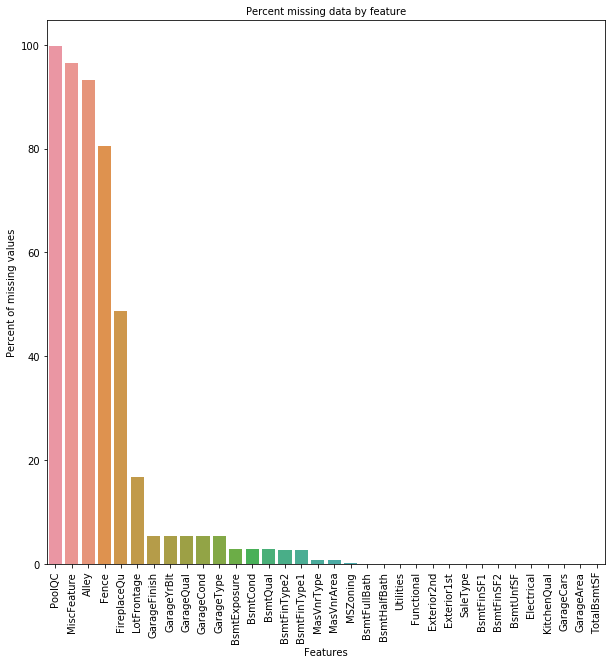
var = 'Utilities' |

var = 'MSZoning' |
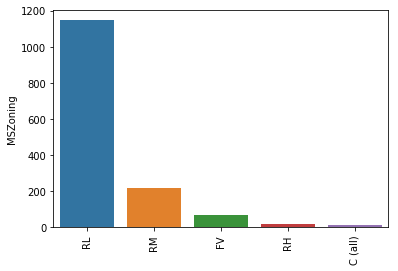
# 填充nil |
data_na = (data.isnull().sum() / len(data)) * 100 |
Series([], dtype: float64)
类型转换,将某些实际是类别类型但用数字表示的强制转换成文本,比如有些调查男表示1,女表示0,在这种情况下,如果我们直接通过dataframe类型判断会导致错误,我们要根据实际情况做转换
#MSSubClass=The building class |
绘制关系矩阵
关系矩阵可以很直观的告诉我们那些变量之间相关,哪些变量并不相关
# 关系矩阵 |
mask = np.zeros_like(corrmat) # 返回相同大小的0矩阵 |
array([[1., 1., 1., ..., 1., 1., 1.],
[0., 1., 1., ..., 1., 1., 1.],
[0., 0., 1., ..., 1., 1., 1.],
...,
[0., 0., 0., ..., 1., 1., 1.],
[0., 0., 0., ..., 0., 1., 1.],
[0., 0., 0., ..., 0., 0., 1.]])
# 绘制热力图 |
<matplotlib.axes._subplots.AxesSubplot at 0x7f8c20d156d8>
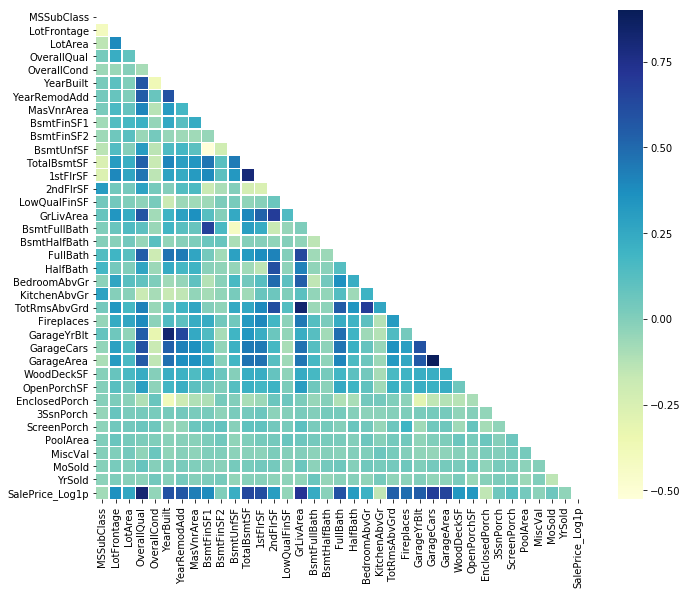
特征工程
对数据做特征变换:
对于类别数据,一般采用LabelEncoder的方式,把每个类别的数据变成数值型;也可以采用one-hot变成稀疏矩阵
对于数值型的数据,尽量将其变为正态分布。
encode_cat_variables = ('Alley', 'BldgType', 'BsmtCond', 'BsmtExposure', 'BsmtFinType1', 'BsmtFinType2', 'BsmtQual', 'CentralAir', |
(2915, 78)
(2915, 343)
# 可以计算一个总面积指标 |
print("Categorical Features: %d"%len(encode_cat_variables)) |
Categorical Features: 46
Numerical Features: 32
数值型变量的分布
#Boxplot for numerical_features |
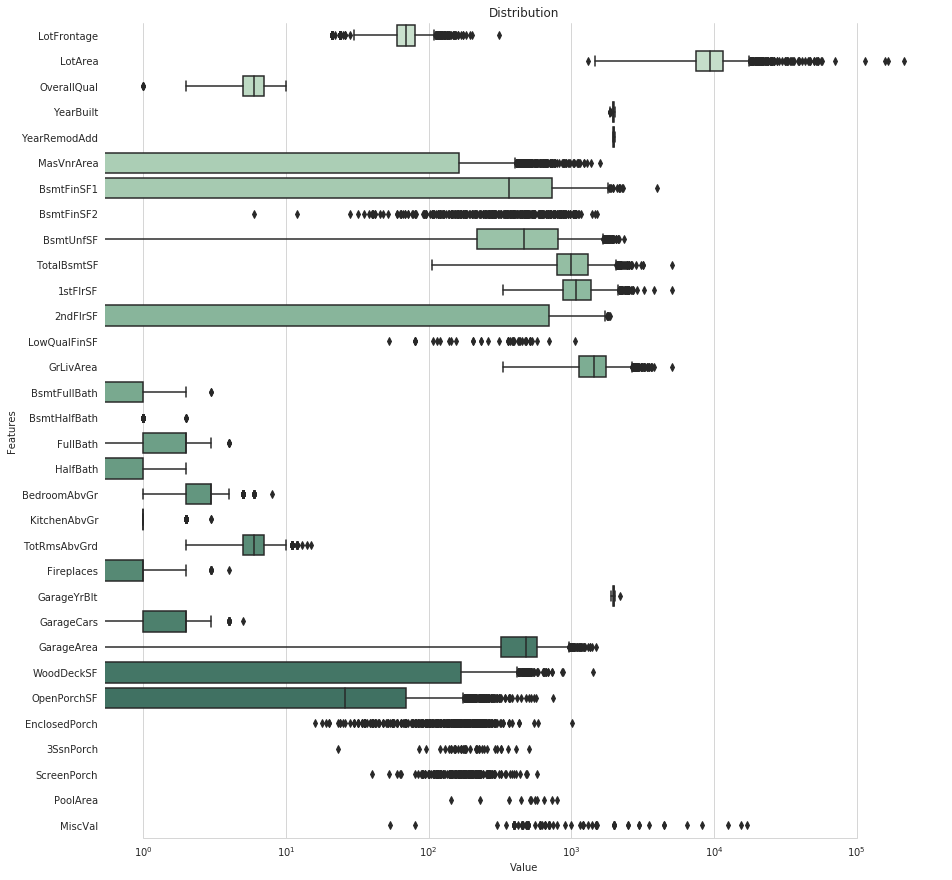
box-cox变换
Box-Cox变换是Box和Cox在1964年提出的一种广义幂变换方法,用于连续的响应变量不满足正态分布的情况。Box-Cox变换之后,可以一定程度上减小不可观测的误差和预测变量的相关性。Box-Cox变换的主要特点是引入一个参数,通过数据本身估计该参数进而确定应采取的数据变换形式
# 计算数值型变量的偏态 |
MiscVal 21.932147
PoolArea 18.701829
LotArea 13.123758
LowQualFinSF 12.080315
3SsnPorch 11.368094
KitchenAbvGr 4.298845
BsmtFinSF2 4.142863
EnclosedPorch 4.000796
ScreenPorch 3.943508
BsmtHalfBath 3.942892
MasVnrArea 2.600697
OpenPorchSF 2.529245
WoodDeckSF 1.848285
1stFlrSF 1.253011
LotFrontage 1.092709
GrLivArea 0.977860
BsmtFinSF1 0.974138
BsmtUnfSF 0.920135
2ndFlrSF 0.843237
TotRmsAbvGrd 0.749579
Fireplaces 0.725958
HalfBath 0.698770
TotalBsmtSF 0.662657
BsmtFullBath 0.622820
BedroomAbvGr 0.328129
GarageArea 0.217748
OverallQual 0.181902
FullBath 0.159917
GarageCars -0.219402
YearRemodAdd -0.449113
YearBuilt -0.598087
GarageYrBlt -3.903046
dtype: float64
skewed_features = skewed_features[abs(skewed_features) > 0.75] |
There are 20 skewed numerical features to Box Cox transform
PoolArea 16.487849
3SsnPorch 8.918476
LowQualFinSF 8.737917
MiscVal 5.592866
BsmtHalfBath 3.798589
KitchenAbvGr 3.695780
ScreenPorch 2.975708
BsmtFinSF2 2.561989
EnclosedPorch 2.023182
TotRmsAbvGrd 0.749579
Fireplaces 0.725958
HalfBath 0.698770
TotalBsmtSF 0.662657
MasVnrArea 0.636713
BsmtFullBath 0.622820
2ndFlrSF 0.329999
BedroomAbvGr 0.328129
WoodDeckSF 0.225571
GarageArea 0.217748
OverallQual 0.181902
LotArea 0.178523
1stFlrSF 0.173668
FullBath 0.159917
GrLivArea 0.102287
OpenPorchSF 0.100679
GarageCars -0.219402
YearRemodAdd -0.449113
BsmtFinSF1 -0.488447
YearBuilt -0.598087
LotFrontage -0.808022
BsmtUnfSF -1.536727
GarageYrBlt -3.922152
dtype: float64
#Boxplot for numerical_features |
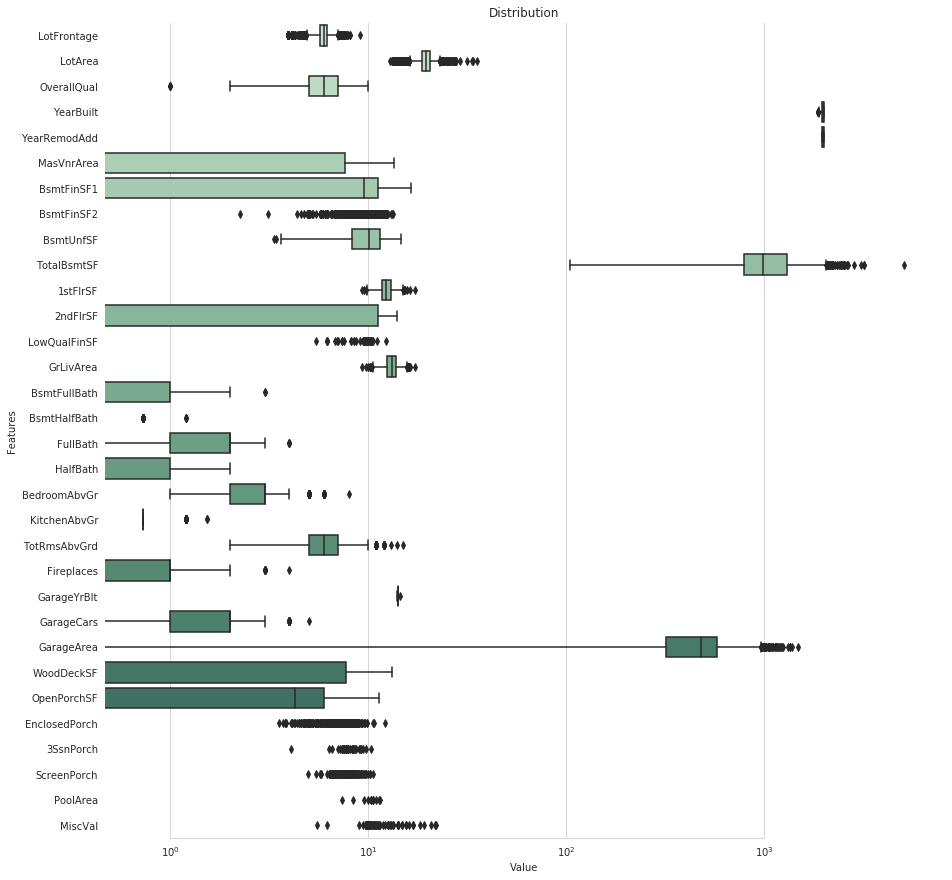
特征处理完后可以将数据再分割开:
train = data[:size_train_df] |
建模
构建算法模型,常用的几个算法模型都试试,然后设置交叉检验:
from sklearn.linear_model import ElasticNet, Lasso, BayesianRidge, LassoLarsIC |
定义一个交叉评估函数
#Validation function |
LASSO回归(LASSO Regression)
采用了L1范数,即绝对值之和。
注:当数据包含许多异常值,使用均值和方差缩放可能并不是一个很好的选择。这种情况下,可以使用 robust_scale 以及 RobustScaler 作为替代品。
lasso = make_pipeline(RobustScaler(), Lasso(alpha =0.0005, random_state=1)) |
Lasso score: 0.1101 (0.0058)
岭回归(Kernel Ridge Regression)
采用了L2范数,即平方和。
KRR = make_pipeline(RobustScaler(), KernelRidge(alpha=0.6, kernel='polynomial', degree=2, coef0=2.5)) |
Lasso score: 0.1152 (0.0043)
弹性网络回归(Elastic Net Regression)
ElasticNet 是一种使用L1和L2先验作为正则化矩阵的线性回归模型,弹性网络是结合了岭回归和Lasso回归,由两者加权平均所得。
https://www.jianshu.com/p/65a573b9fe32
ENet = make_pipeline(RobustScaler(), ElasticNet(alpha=0.0005, l1_ratio=.9, random_state=3)) |
Lasso score: 0.1100 (0.0059)
组合模型
现在常用的组合模型有提升树(Gradient Boosting Regression)、XGBoost、LightGBM 等
提升树(Gradient Boosting Regression):
GBoost = GradientBoostingRegressor(n_estimators=3000, learning_rate=0.05, |
Lasso score: 0.1164 (0.0082)
XGBoost
model_xgb = xgb.XGBRegressor(colsample_bytree=0.4603, gamma=0.0468, |
Lasso score: 0.1172 (0.0053)
LightGBM
model_lgb = lgb.LGBMRegressor(objective='regression',num_leaves=5, |
Lasso score: 0.1162 (0.0060)
寻找最优参数
通过可视化的方式来看看如何寻找模型最优参数
alphas = [0.00005, 0.0001, 0.0005, 0.001, 0.005, 0.01] |
cv_ridge = pd.Series(cv_ridge_score, index = alphas) |
Text(0, 0.5, 'rmse')
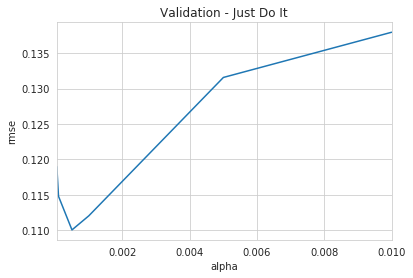
几个基础模型预测值的比较:
train_size = int(len(train)*0.7) |
Pipeline(memory=None,
steps=[('robustscaler', RobustScaler(copy=True, quantile_range=(25.0, 75.0), with_centering=True,
with_scaling=True)), ('elasticnet', ElasticNet(alpha=0.0005, copy_X=True, fit_intercept=True, l1_ratio=0.9,
max_iter=1000, normalize=False, positive=False, precompute=False,
random_state=3, selection='cyclic', tol=0.0001, warm_start=False))])
残差图
preds = pd.DataFrame({"preds":GBoost.predict(X_test), "true":y_test}) |
<matplotlib.axes._subplots.AxesSubplot at 0x7f8c1a72aef0>
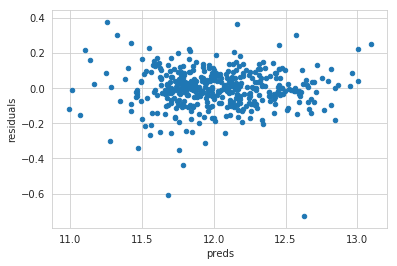
preds = pd.DataFrame({"preds":ENet.predict(X_test), "true":y_test}) |
<matplotlib.axes._subplots.AxesSubplot at 0x7f8c1a6ed128>
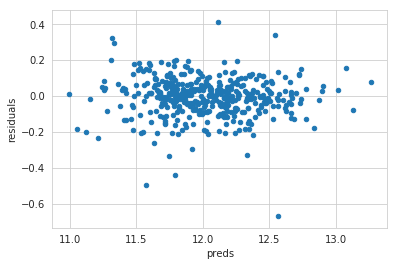
xgb_preds = np.expm1(GBoost.predict(X_test)) |
<matplotlib.axes._subplots.AxesSubplot at 0x7f8c00ba9d30>
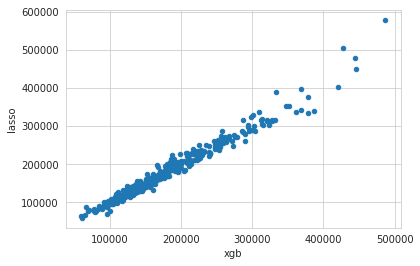
集成学习(模型融合)
Stacking models 是指通过将多个模型进行集成以取得更小预测方差的方法, 通过前面的两个模型残差图的分布可以发现具有一定的互补性,所以这才是融合的目的,将他的残差分布变得更均匀。
平均模型
class AveragingModels(BaseEstimator, RegressorMixin, TransformerMixin): |
averaged_models = AveragingModels(models = (ENet, GBoost, KRR, lasso)) |
Averaged base models score: 0.1081 (0.0056)
堆叠模型(Stacking Averaged Models)
其由两部分组成,一部分是基准模型,一部分是回归模型:
基准模型和大量数据组合预测一堆结果,然后根据预测结果通过回归模型预测和真实值的差异。具体如下: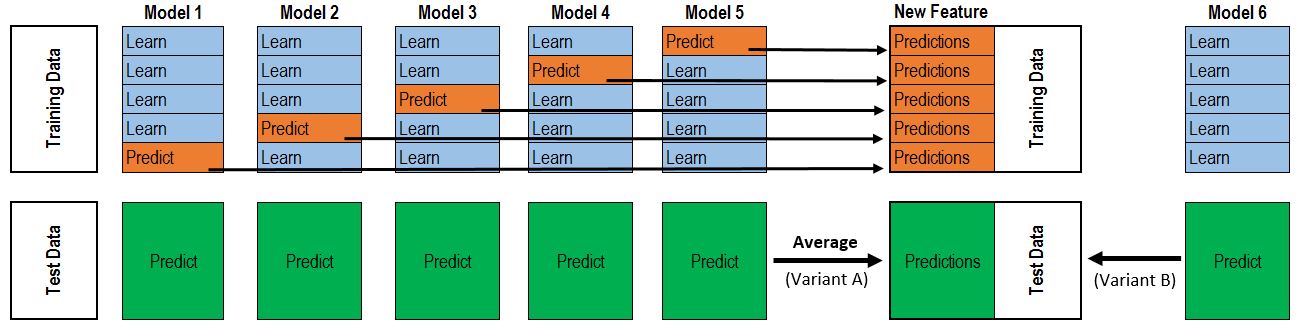
class StackingAveragedModels(BaseEstimator, RegressorMixin, TransformerMixin): |
from sklearn.linear_model import LinearRegression |
Stacking Averaged models score: 0.1086 (0.0060)
参考资料
https://www.kaggle.com/serigne/stacked-regressions-top-4-on-leaderboard
https://www.kaggle.com/jolasa/eda-anda-data-preparation-7th-place
https://www.kaggle.com/apapiu/regularized-linear-models

